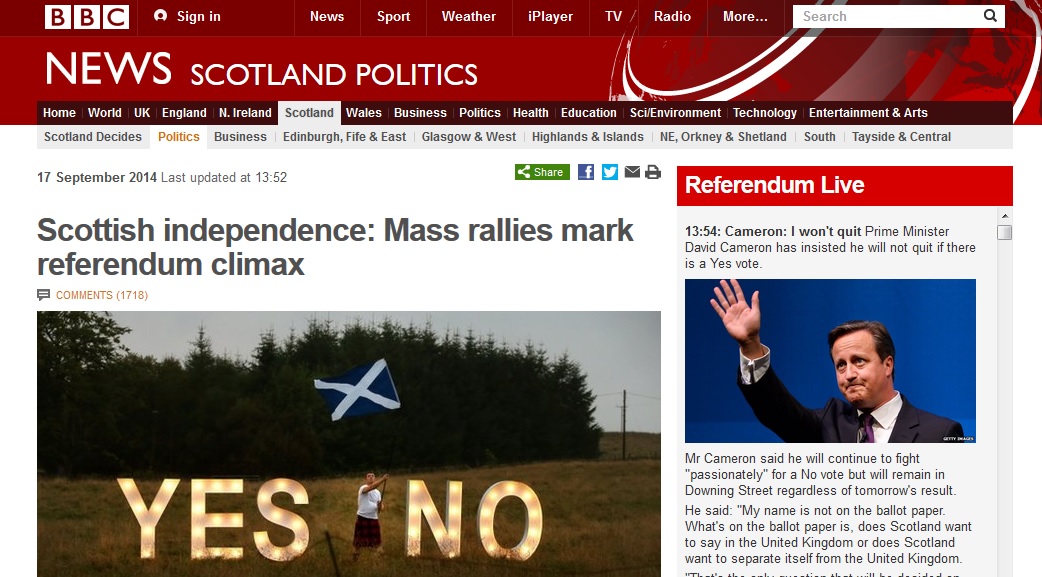
As a pedant of a scientific bent, I'm seizing this eve-of-Scottish-referendum moment to try to explain - simply, I trust - the basics of opinion polls, specifically sample size and accuracy.
For an opinion poll to be believable, at least two conditions must be fulfilled.
First, the people being polled - the sample - must be representative of the wider population as far as possible, on criteria such as anno domini and gender. Or, as we self-appointed wags like to say, appropriately broken down by age and sex. This is known in the political polling trade - psephology - as "weighting".
Second, the sample needs to be of sufficient size to tease out any significant trend in the sample, and hence the population. Hold on to your school desks, children, as I take you through this tiny step by step.
It is logical that the smaller the sample, the dodgier the conclusion. If I have a crowd of representative Scots crammed on to a football pitch and ask only the bloke on one of the penalty spots for his voting intentions in the #indyref, I may conclude that there will be a 100 per cent Yes, No or Don't Know result when the referendum refs blow their whistles for full time tomorrow night.
The trick with sampling is to poll the smallest number of people you need to get a meaningful - that is, "statistically significant" - result. Asking a million people for their opinion when you only need to ask 10,000 will waste time and money. So far, so bleeding obvious.
Now for the tiny bit of maths. The magic phrase to grasp is "1 over the square root of n". That is how you calculate how much you can trust the result of an opinion poll, where n is the size of the sample: what pollsters call the error.
Suppose, foolishly, you poll only nine people from your sample on the simple Yes/No question "Do you ever wear a kilt?" and don't allow any Don't Knows. You calculate the error as 1 divided by the square root of 9; that is, 1 divided by 3. So the error is 1/3 - a third, or 33.33333 etc per cent. Not much Kop, in footballing parlance, and deserving of a statistical yellow card.
Most reputable polling organisations go for samples of 1,000 - in which case, the error is about 1/32, around 3.1 per cent - or spend more for samples of 1,500 (error about 2.5 per cent), or even 2,000 (error about 2.2 per cent).
So if I can poll a weighted sample of 1,000 in Sutherland, my favourite rural destination in Scotland, and 73 per cent say they sometimes wear a kilt, I can be confident I have obtained a statistically significant result.
The calculated error of 3.1 per cent suggests that my figure for kilt wearers could be as small as about 70 per cent or as high as 76 per cent. The 27 per cent figure for those who say they never wear a kilt could be as high as 30 per cent or as low 24 per cent. The difference between the two responses is said to be "statistically significant" and I can have high confidence I am not talking sporran-adjacent nonsense.
I hope this explains why there can be controversy when a sample size in an opinion poll about #indyref voting intentions is only 500, with an error of about 4.5 per cent. If I obtain a 54-46 split from my sample, the ranges can be 58 to 50, and 42 to 50, respectively. I cannot have great confidence that I am sampling anything other than error in my methodology.
Anyway, come Friday morning, the opinion polls and their sampling errors will be ancient history because - as we all know in that politician's cliché - it's only the real vote that counts. Until the next opinion poll, anyway.

 RSS Feed
RSS Feed


